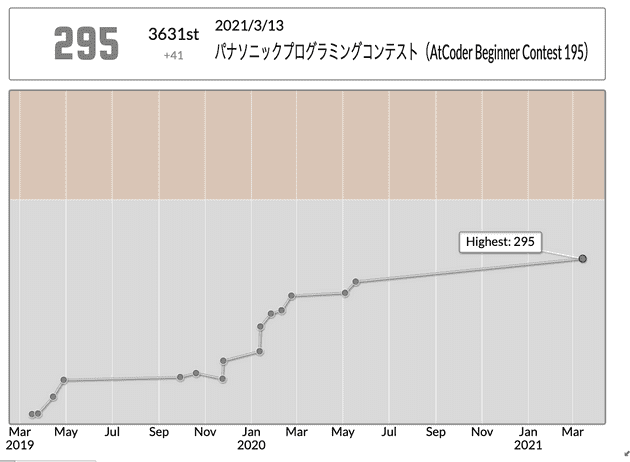
競プロを最近頑張ってるので、「パナソニックプログラミングコンテスト（AtCoder Beginner Contest 195）」に出てみました。

結論言うと、過去最高のパフォが出て嬉しかったです。この調子だと灰色は後3~4回で抜けれそう。 灰色ってあんまり競プロやってますって胸張って言えない感じあるので茶色までとりあえず頑張ります。

終わってまだ1時間も経ってませんが、覚えてるうちに解けたとこだけでも振り返ってみます。

A問題

HがMかどうか判定しましょう。即答できて嬉しかった。

ans = "No"
if (H % M == 0):
    ans = "Yes"

B問題

A <= みかんの重さ <= B　のみかんがいっぱいある。 いくつかみかんを選んだら重さの合計がちょうどWキログラム。 みかんの個数の最小値と最大値を求める起こり得ないならそのことを報告してください（UNSATISFIABLE）。

多分一番悩みました。結果40分くらいかけてしまった。伸びしろですね。

どんな時にUNSATISFIABLEになるかがよく理解できず、色々考えました。 結論、重要なのは「AとBの重さの差」だと思います。

最大値の時の考え方は、

• W // Aを考える（ans_maxとする）
• あまりがdグラムだとすると、「AとBの重さの差」の範囲でみかんをいくつか(最大でans_min個まで)重くしてあまりdを吸収することを考える

つまり、d <= d * ans_minに収まればOK,そうでないならもうUNSATISFIABLEのはず。

最小値の時も焦ってこの考え方に当てはめようとしてミスったのですが、最小値の時はちょっと違いますね。（落ち着けばわかるけど、、）

• W // Bを考える（ans_maxとする）
• あまりがdグラムだとすると、「AとBの重さの差」の範囲でみかんをいくつか(最大でans_max個まで)軽くして、あまりdと軽くした分でもう一つみかんを追加すること考える（あまりが無ければ追加は当然しない）

これを実装すると良いです。こう見るとシンプルで、これを安定して10分ちょいで解けるようになりたい。

C問題

高橋君は整数を書くとき、下から 3桁ごとにコンマで区切って書きます。例えば 1234567であれば 1,234,567、777であれば 777 と書きます。 高橋君が1以上N以下の整数を1度ずつ書くとき、コンマは合計で何回書かれますか？

これちょっと怖かったのが、1≤N≤10**15なんですよね。
高橋くんカワイソウすぎる笑

max_count_5_case = 1
max_count_4_case = (10**15-1) - (10**12 - 1)
max_count_3_case = (10**12-1) - (10**9 - 1)
max_count_2_case = (10**9-1) - (10**6 - 1)
max_count_1_case = (10**6-1) - (10**3 - 1)

if length == 16:
    ans = max_count_5_case*5 + max_count_4_case*4 + \
        max_count_3_case*3 + max_count_2_case * 2 + max_count_1_case

# max4回の範囲
elif 13 <= length <= 15:
    ans += max_count_3_case*3 + max_count_2_case * \
        2 + max_count_1_case + 4 * (N - (10**12 - 1))

# max3回
elif 10 <= length <= 12:
    ans += max_count_2_case * \
        2 + max_count_1_case + 3 * (N - (10**9 - 1))

elif 7 <= length <= 9:
    ans += max_count_1_case + 2 * (N - (10**6 - 1))

elif 4 <= length <= 6:
    ans += N - (10**3 - 1)

桁数に応じてグループ分けして、グループの中で何番目の数字か（＝同じグループの数字を何回書く必要があるか）を引き算します。 Bより簡単じゃない？って気もしますが、これもなんだかんだ40分くらい掛けてしまってます。境界を間違えてだいぶテンパりました。

D問題以降

解けてません！C終わった時点で80分なので無理です。 Dだけチラッとみたのですが、ナップサックっぽかったですね。DP使って解くのだろうか？知らんけど。